[コンプリート!] 球 体積 求め方 243996-球 体積 求め方 積分
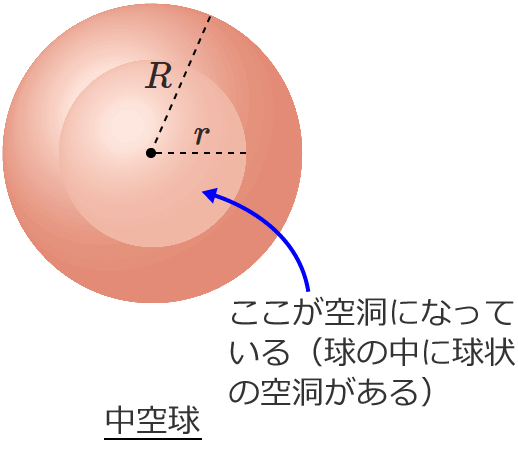
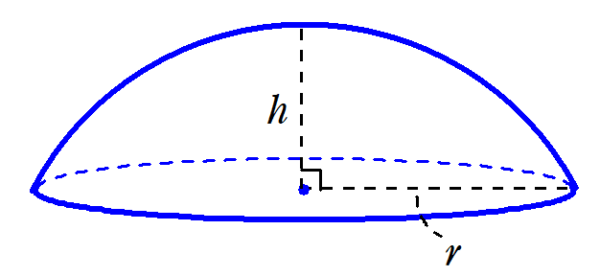
球欠の体積よりもさらにシンプルな式です。 こちらについても、まずは半球を使って確認してみましょう。 例2 <図8> 半球 この半球は、切り口の円の半径 r = R ~r=R~ r = R 、切り口の円の中心から球冠までの距離 h = R ~h=R~ h = R の球欠とみなすことができる
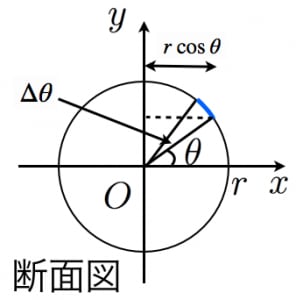
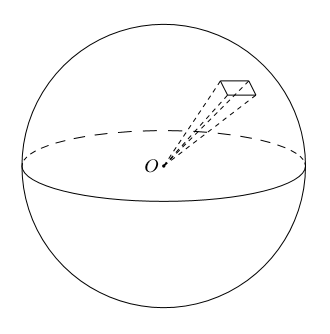
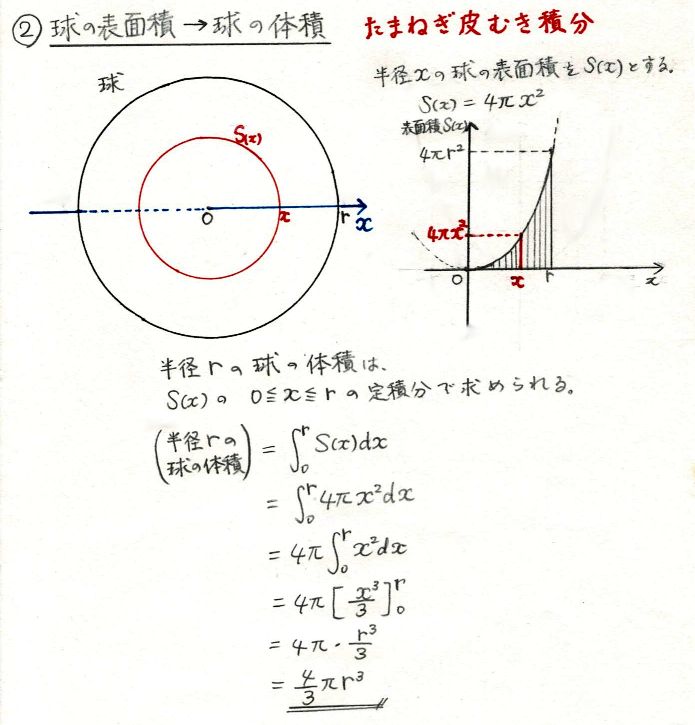
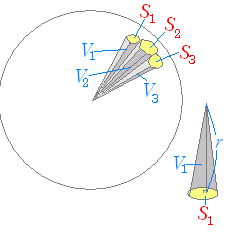
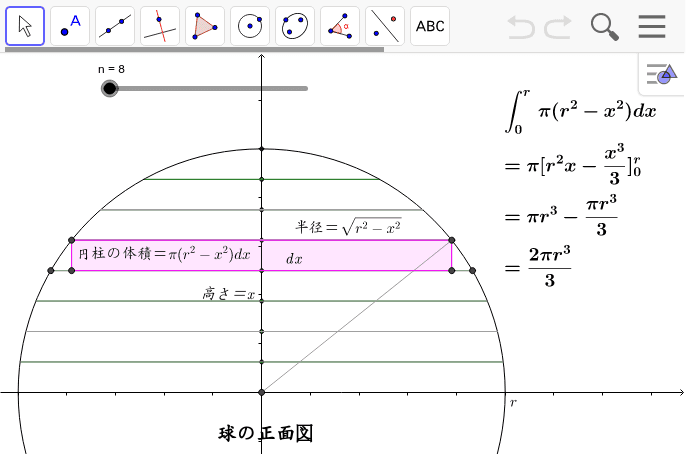
球 体積 求め方 積分- 目的 「楕円の面積」や「楕円体の体積」の求め方を紹介します。 理解のためのステップ ステップ ステップとして下記のステップを踏んで「4楕円体の体積」を求めたいと思います。 1円の面積 2楕円の面積 3球の体積 求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える. 幅は 、長さは なので, より微小な角度を考える 球全体で積分する 計算 求め方2:球の体積を用いる方法 考え方 半径 の球の表面積を とおく
球 体積 求め方 積分のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 | ||
 |  | |
「球 体積 求め方 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「球 体積 求め方 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「球 体積 求め方 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
 |  | |
「球 体積 求め方 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「球 体積 求め方 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「球 体積 求め方 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「球 体積 求め方 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「球 体積 求め方 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 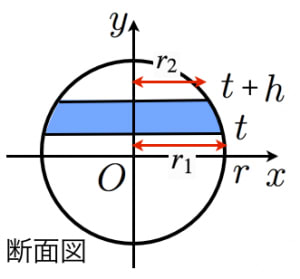 |
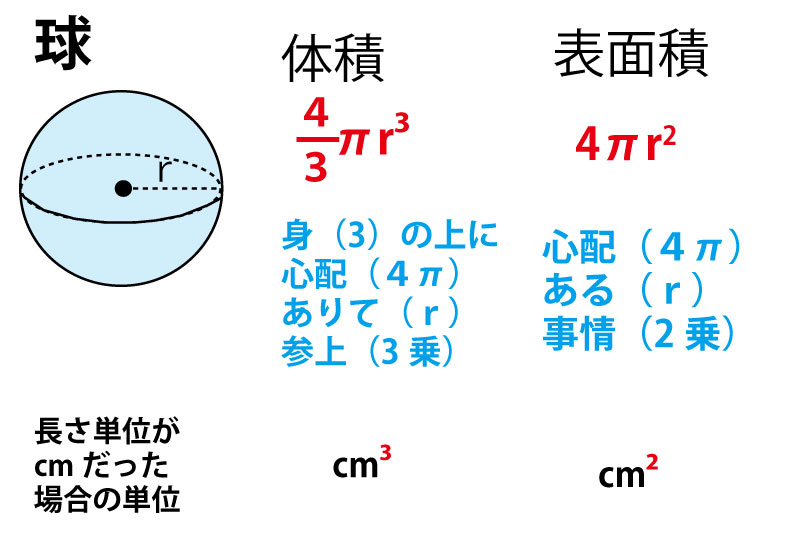
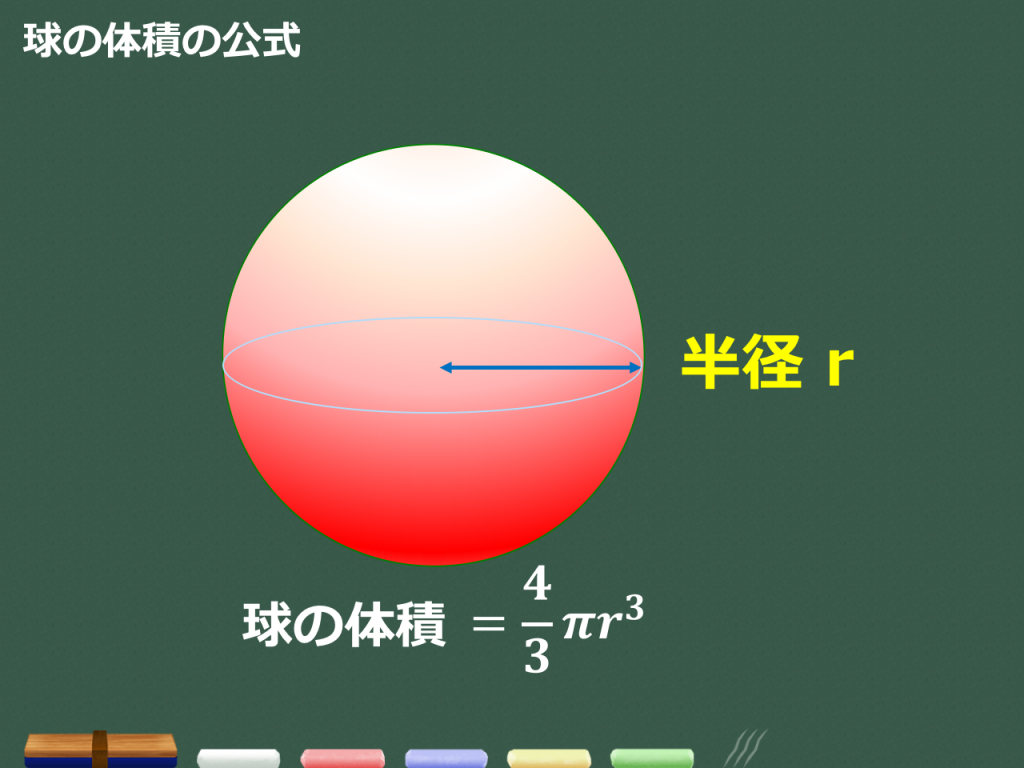
全体積 V x v R j j j x ∑ = x成分を求める x a b x 位置xで切断し た断面の面積を S(x)とする S (x) ∆ x この板では x座標は「一定」で x j この体積が v j =S(x)∆ x この和を薄い円板 の分割和と考える 工学院大学の学生のみ利用可:印刷不可:再配布 球の体積の公式とその覚え方・語呂合わせ 球の体積の公式 球の体積を求める公式は以下の通りです。 球の体積は半径rのとき、 \(\frac{4}{3}πr^3\) となります。 球の体積の証明のためには積分を利用する必要があり、少し難易度が高くなっています。
Incoming Term: 球 体積 求め方, 球 体積 求め方 重積分, 球 体積 求め方 原理, 球 体積 求め方 積分, 球 体積求め方 例題,
コメント
コメントを投稿